Research

Structure preserving discretization of port-Hamiltonian systems

Since my PhD I have been working on structure preserving methods for port-Hamiltonian systems. To this aim I have primarily used open-source finite element librairies like FEniCS and Firedrake but I also developed my own code for simple simulations.

• Finite element exterior calculus and port-Hamiltonian dynamics

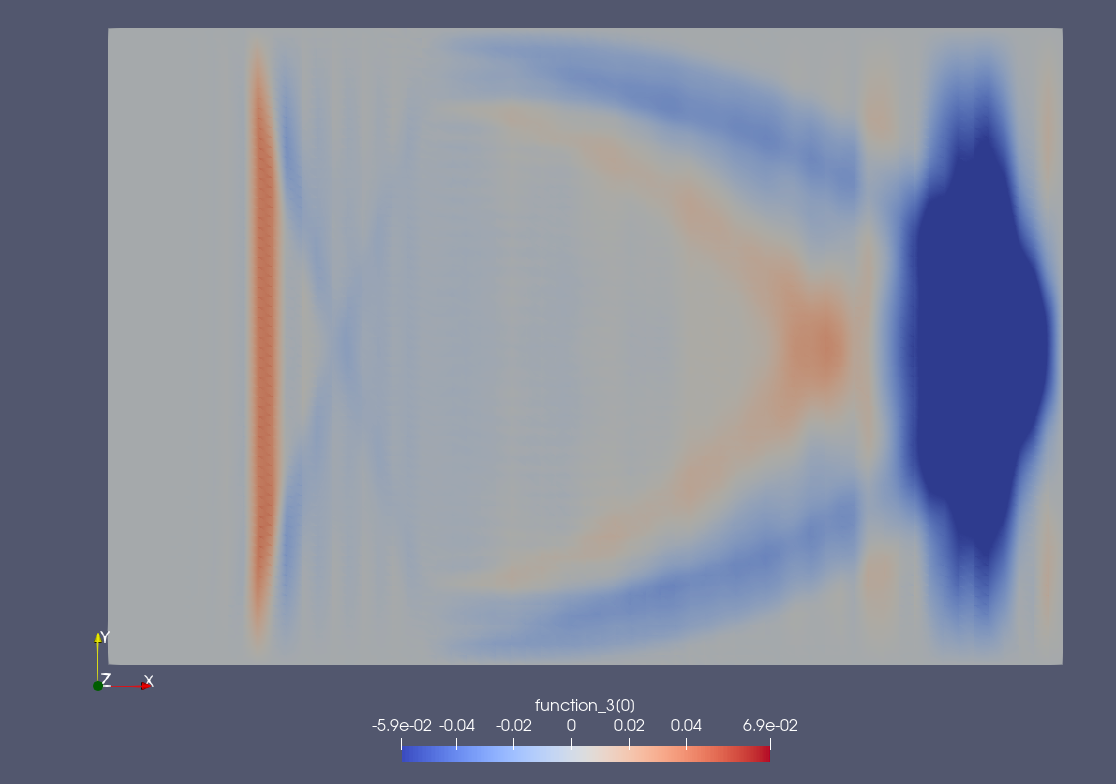
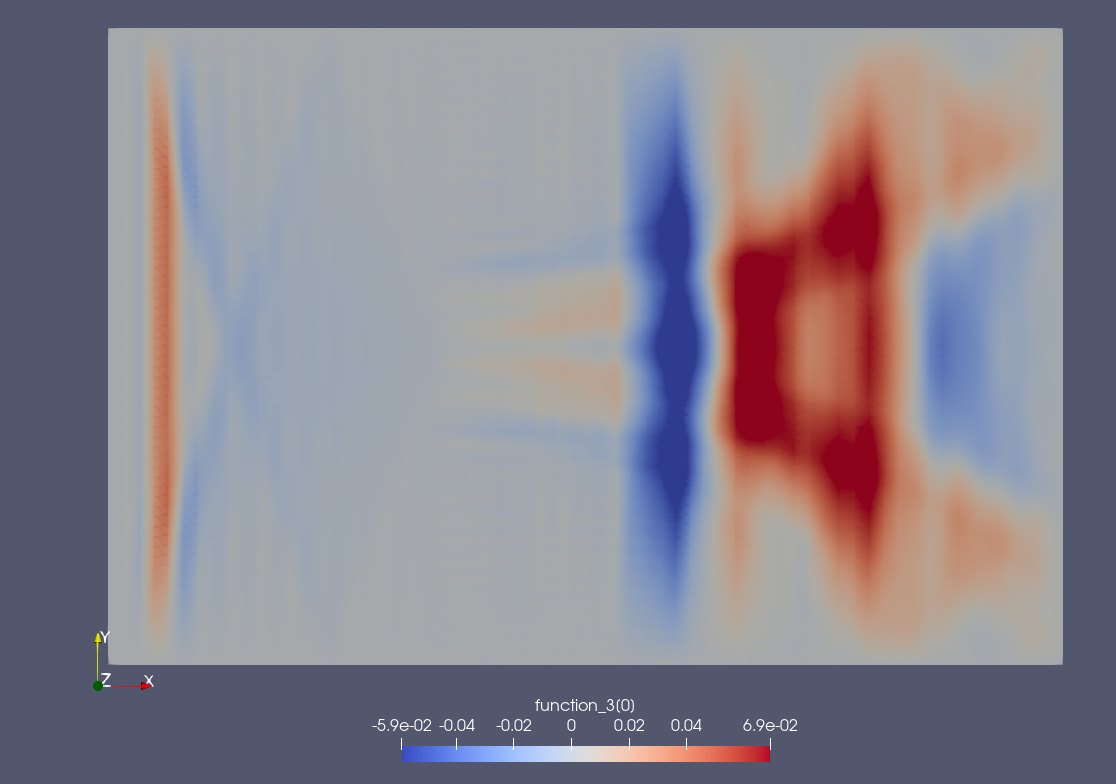
Physical equations are typically written using vector calculus but they can also be written using the language of differential geometry. This latter formalism distiguishes topological and metrical notions and connects integration, derivation using coordinate free expressions. Seemingly different numerical methods (e.g. finite differences, finite elements, finite volumes) can be understood in a unified way when described using tools from differential geometry. Hamiltonian and port-Hamiltonian systems are tipically formulated in a geometric setting. In my research I have established general methodologies on how to discretize port-Hamiltonian systems using Finite Element Exterior Calculus.

Pressure at \(t=2\,[\mathrm{s}]\)

Pressure at \(t=3\,[\mathrm{s}]\)

Figure 1: Snapshots of the pressure for an Heterogeneous domain using an hybrid finite element formulation.

• Structural dynamics and integrators In nonlinear mechanics, energy preserving method are preferred as they produce stable and accurate simulations. However this method are tipically implicit and they require Newton iterations to produc a solution. By reformulating the equations, linearly implicit energy conserving method can be devised. For instance, consider the oscillator in Figure 2. The system corresonds to the famous duffing oscillator.

Figure 2: Geometrically nonlinear oscillations of a sliding mass

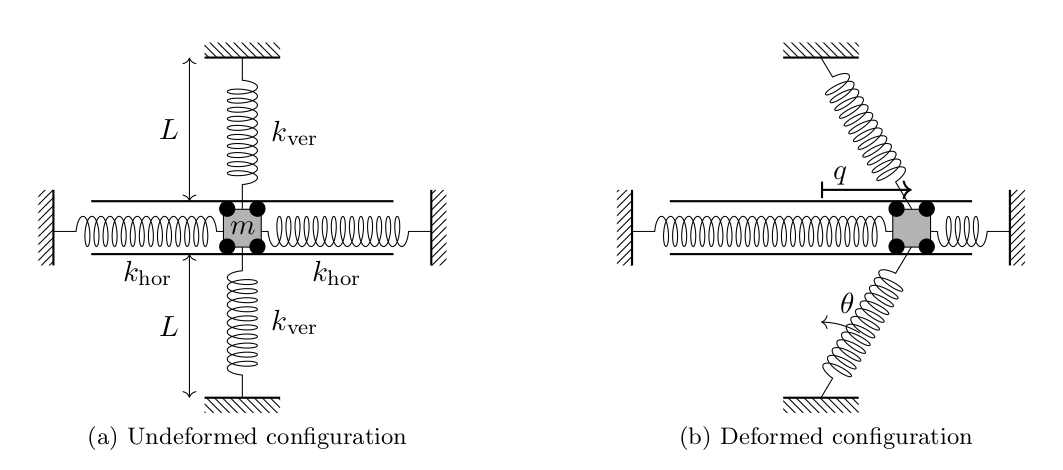
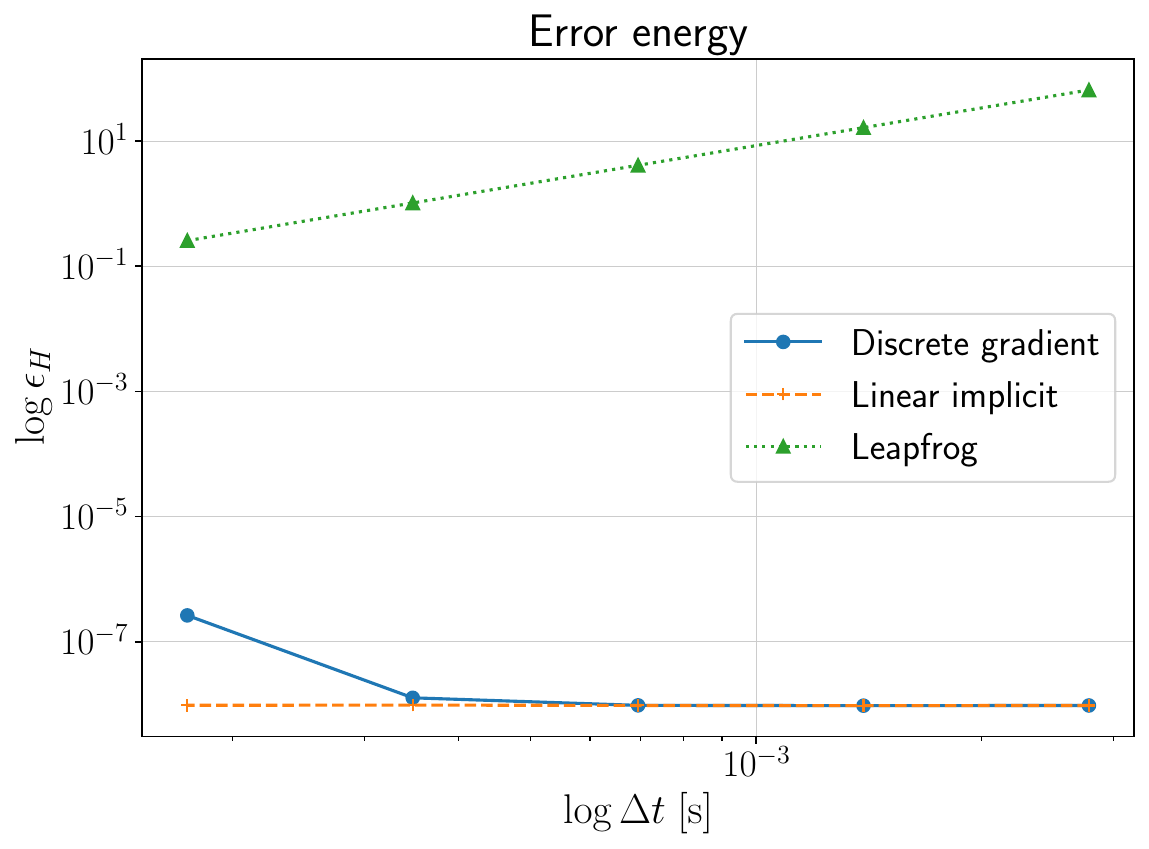
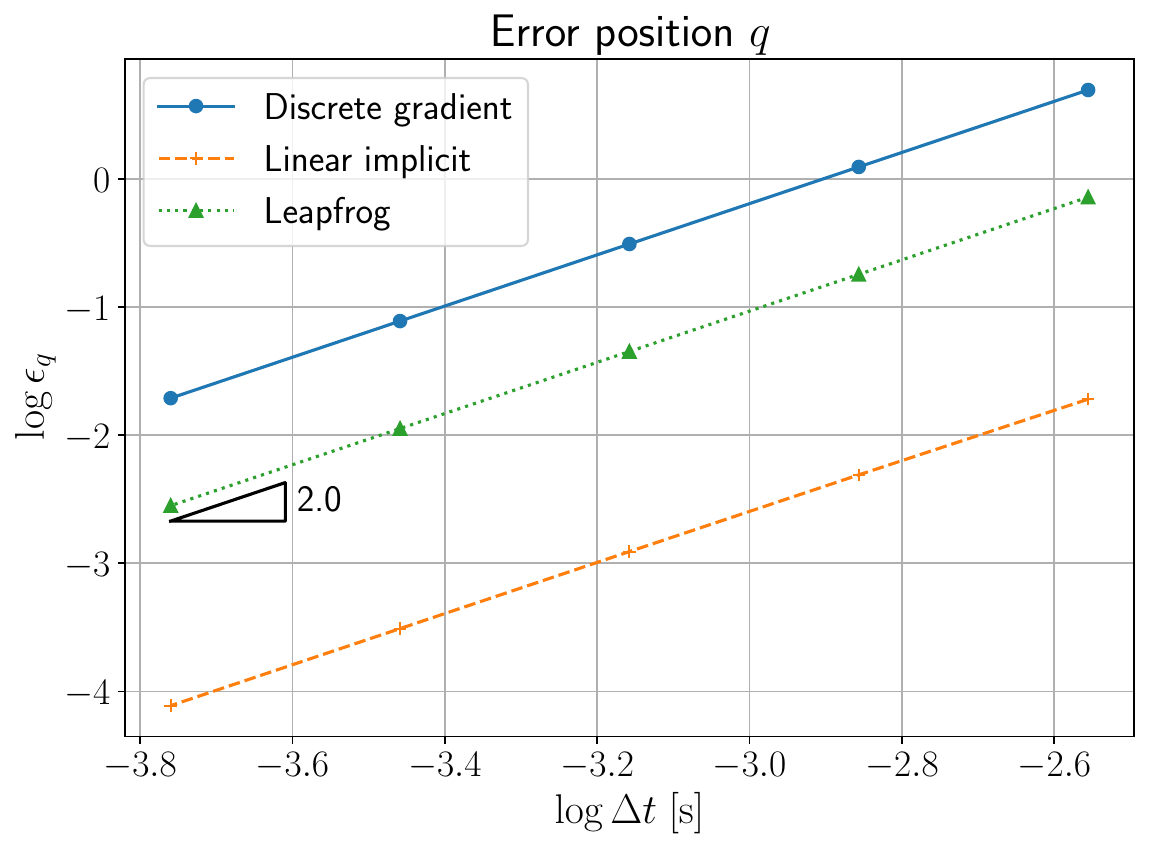
The intergration is capable of preserving the energy exactly and has a lower error with respect to other integrators Figure 3.

Energy error

Error on the position of the mass

Figure 3

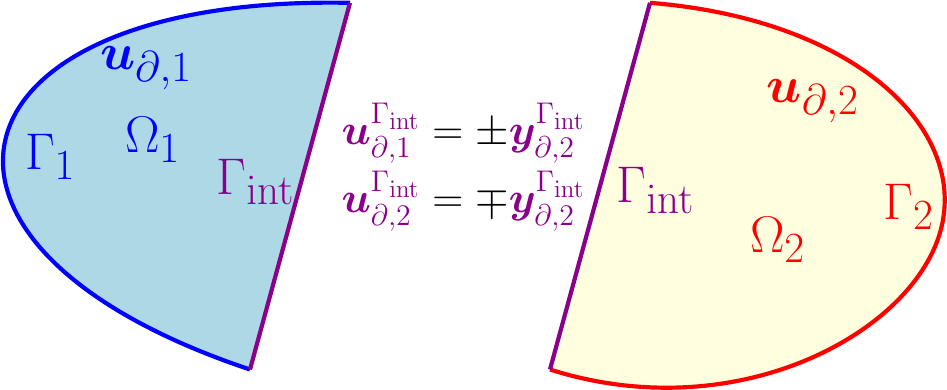
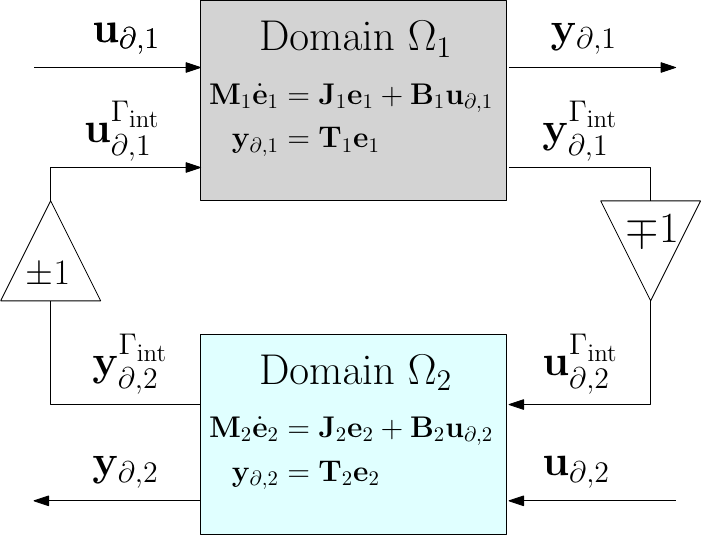
• Systems theory and numerical methods System theory provides a structural way of thinking about interconnected system. This can be used to reinterpret numerical method that uses local basis glued together in a strong or weak way. Numerical fluxes in discontinuous methods may benefit from such an interpretation.

Splitting of the domain

Interconnection at the interface

Feedback interconnection

Figure 4: Numerical fluxes as feedback interconnection.

Numerical methods for high frequency structural dynamics

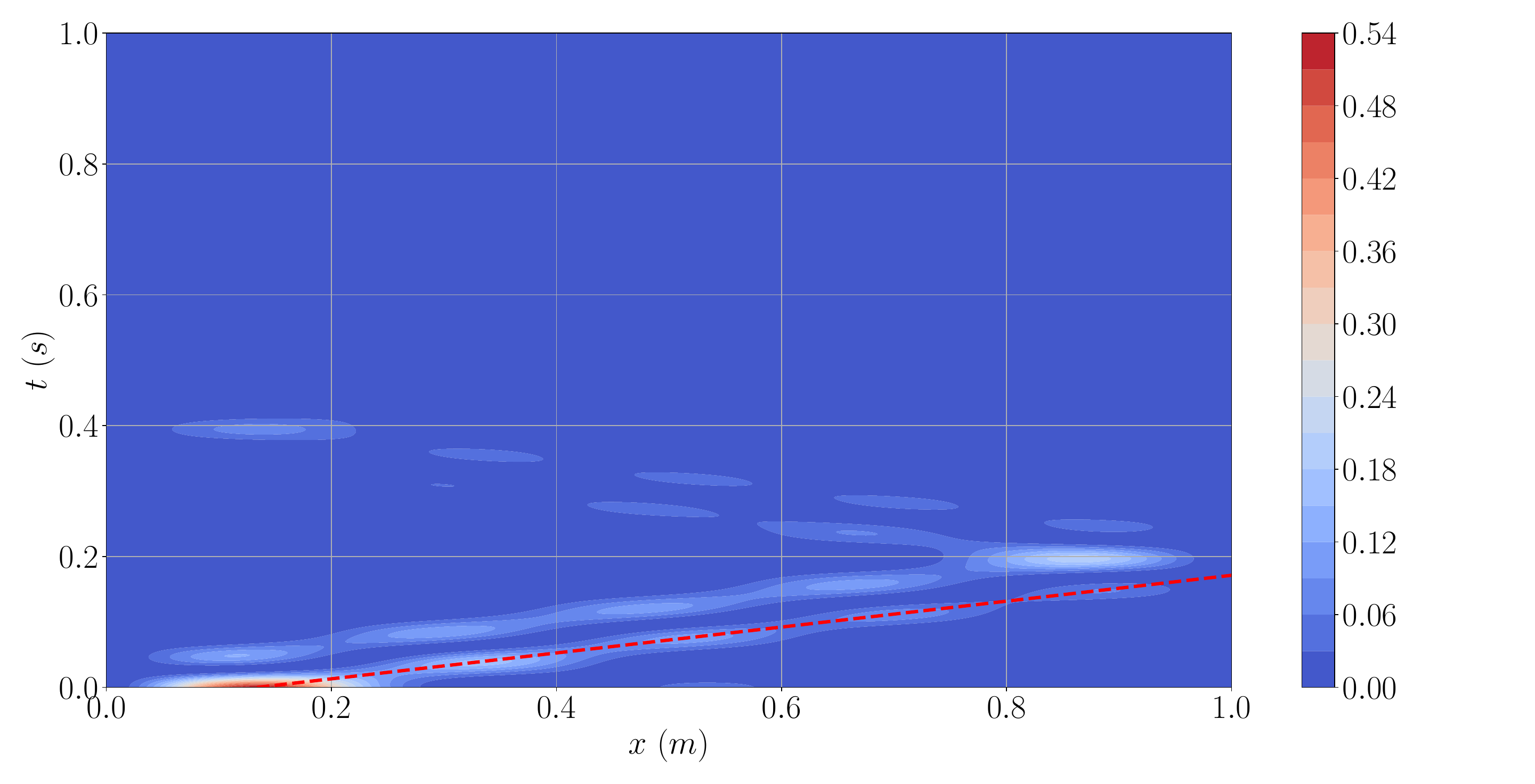
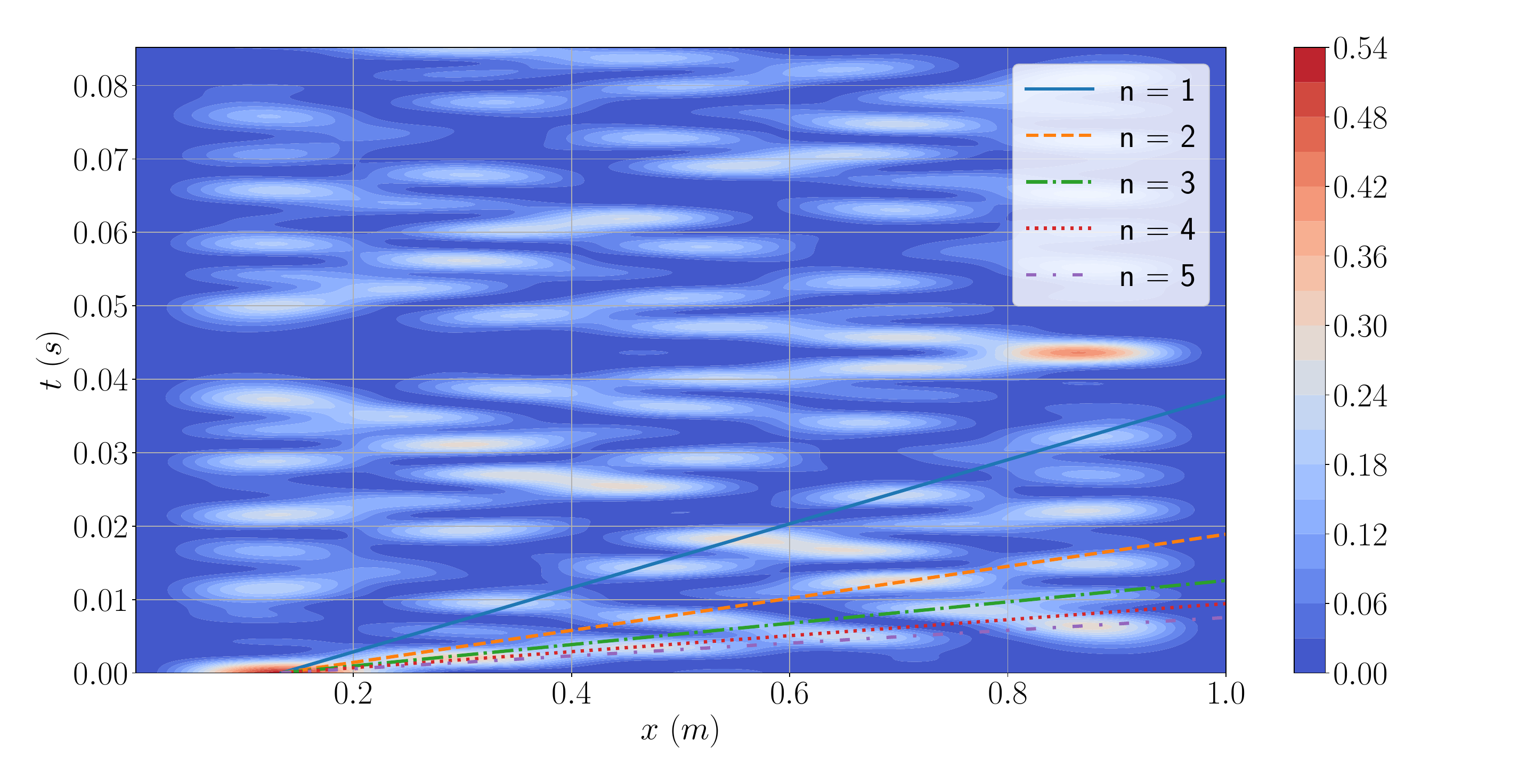
Classical finite elements notorously struggle when high frequency waves propagate in solids. Alternative methods can be used to tackle this problem, like Treffz method or statistical energy analysis.

Figure 5: Waves in a nondispersive solid

Figure 6: Waves in dispersive solid is more difficult to track as grouph and phase velocities are different